Basisbegrippen
Op deze pagina leggen we kort een aantal basisbegrippen uit die regelmatig terugkomen op de Network Pages. Wie meer wil weten, verwijzen we naar de uitgebreide Wikipedia-artikelen over deze begrippen.
Veel alledaagse fenomenen kunnen beschreven worden door netwerken. Neem bijvoorbeeld filevorming op landelijk niveau. Het wegennetwerk beschrijft de mogelijke routes die het auto- en vrachtverkeer kunnen nemen, en geeft de maximale verkeersstroom aan die verwerkt kan worden. Een elektriciteitsnetwerk beschrijft hoe stroom kan lopen. Een vriendennetwerk beschrijft wie met wie kan praten om nieuws of roddels te verspreiden. Veel onderdelen van de onmisbare infrastructuur van onze maatschappij kunnen door middel van netwerken beschreven worden, en netwerken vormen daarom een belangrijk onderzoeksveld. In de Network Pages zijn verschillende voorbeelden van zulk onderzoek te vinden.
Een netwerk bestaat uit objecten die onderling verbonden zijn, en mogelijk ook uit de eigenschappen van de objecten en hun verbindingen. In een wegennetwerk kunnen de objecten de steden zijn en de verbindingen de wegen. De eigenschappen van objecten kunnen de aantallen auto’s in de steden betreffen, en de eigenschappen van de verbindingen de lengtes van de wegen, het aantal rijbanen, de hoeveelheid verkeer, etc. De objecten en hun onderlinge verbindingen worden weergegeven als ‘grafen’, zie onderstaande uitleg. In computernetwerken zijn de computers de objecten, met elkaar verbonden door middel van fysieke kabels. Eigenschappen van de verbindingen kunnen zijn de bandbreedte van de kabels, de hoeveelheid data die via de kabels verzonden worden, of zelfs de vertraging die de datapakketten oplopen als ze verstuurd worden.
Maatschappelijke uitdagingen vereisen vaak dat netwerken beheerst en ontworpen worden om zo efficiënt mogelijk te functioneren. Hiervoor worden vaak algoritmes gebruikt, zie uitleg. Onvoorspelbaarheid en afwijkingen, bijvoorbeeld in de hoeveelheid verkeer op een wegennetwerk, komen regelmatig voor in netwerken. Een betrouwbare aanpak om met onzekerheden om te kunnen gaan, is cruciaal voor het oplossen van vele maatschappelijke problemen. Daarom speelt, naast de theorie van algoritmes, kansrekening een belangrijke rol bij het onderzoek naar netwerken.
Zoals eerder uitgelegd, bestaat een netwerk uit objecten die onderling verbonden zijn. Wiskundigen noemen zo’n netwerk een graaf, en de objecten knopen (of vertices), en de verbindingen kanten. Als we bijvoorbeeld een sociaal netwerk van een groep mensen weergeven als een graaf, dan zijn de knopen de mensen waar het om gaat, en beschrijven de kanten hun onderlinge relaties. Dus, als Anne en Bob twee vrienden zijn in het sociale netwerk, dan bevat de graaf een “Anne”-knoop en een “Bob”-knoop met een kant ertussen.
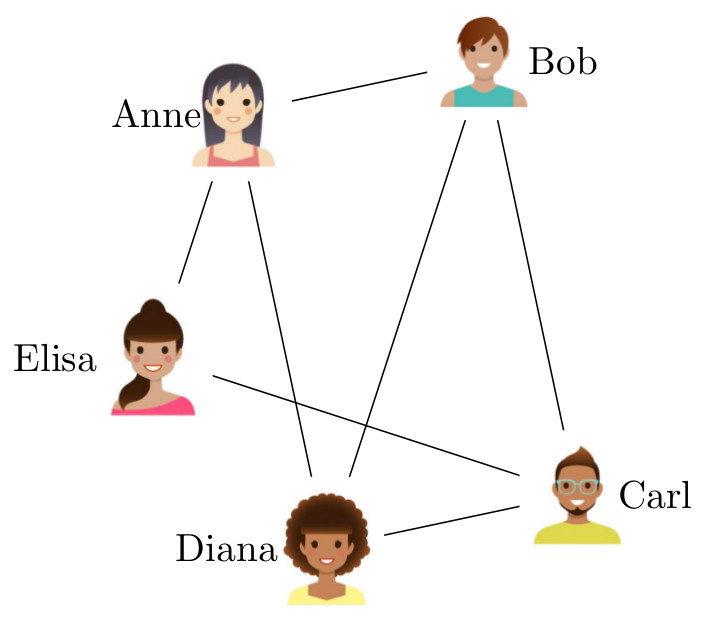
Een eenvoudig netwerk van vijf mensen. Wanneer twee mensen vrienden zijn, zijn ze verbonden door middel van een kant. Plaatjes ontworpen met behulp van Freepik.
In treinnetwerken staan de knopen voor de treinstations en de kanten voor de spoorlijnen waarmee ze onderling verbonden zijn. Uiteraard zijn we soms ook geïnteresseerd in de eigenschappen van de objecten en hun verbindingen, maar daar gaan we nu nog niet op in.
We noemen nog enkele voorbeelden van netwerken. In het netwerk van Facebookvriendschappen staan de knopen voor Facebookgebruikers en trekken we kanten tussen Facebookvrienden. In het netwerk van acteurs die opgenomen zijn in de Internet Movie DataBase (IMDB) staan de knopen voor de acteurs en tekenen we kanten tussen iedere twee acteurs die samengewerkt hebben in een film. In een graaf van het internet kunnen de knopen staan voor routers en de kanten voor fysieke kabels die routers met elkaar verbinden. In het World-Wide Web staan de knopen voor webpagina’s en de kanten voor de hyperlinks waarmee ze verbonden zijn. Soms kunnen datasets door middel van meerdere netwerken weergegeven worden. In het voorbeeld van het IMDB kunnen we ook de films als knopen beschouwen en een kant tekenen tussen twee films als een acteur in beide heeft gespeeld. Verschillende netwerkweergaves kunnen inzicht bieden in de verschillende eigenschappen van datasets.
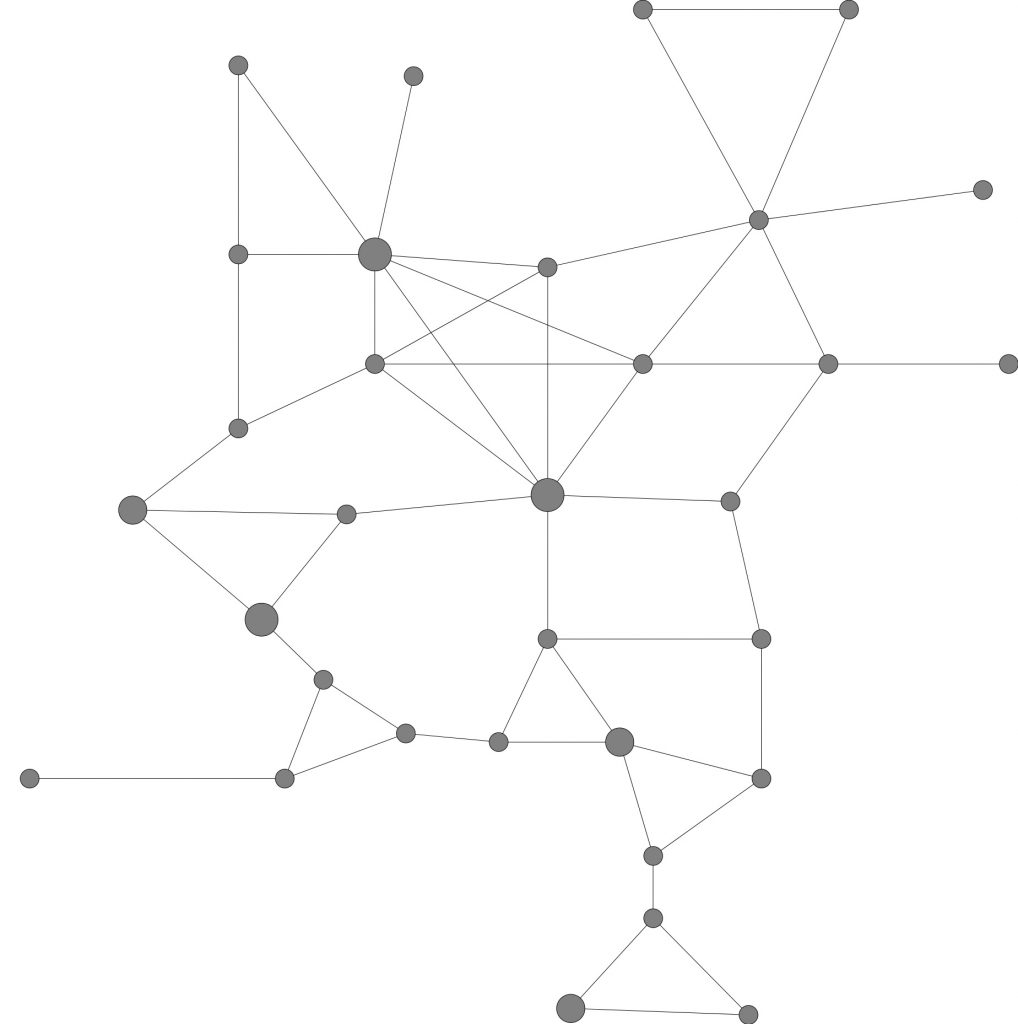
Weergave van het vereenvoudigde Nederlandse spoornetwerk. De knopen zijn hier treinstations, onderling verbonden door spoorlijnen.
In veel netwerken hebben de verbindingen een richting die van belang is. In een wegennetwerk bijvoorbeeld is het best belangrijk om de rijrichting van het eenrichtingsverkeer te weten!
Laten we nu enkele basisbegrippen uit de grafentheorie bespreken. De graad van een knoop is het aantal verbindingen dat het heeft, of, in andere woorden, het aantal kanten waar het deel van uit maakt. Een graaf wordt samenhangend genoemd als het mogelijk is om tussen ieder tweetal knopen te bewegen door van knoop naar knoop te springen. De graafafstand tussen twee knopen is het kleinste aantal kanten tussen die knopen, of het kleinste aantal stappen dat genomen moet worden van start- naar eindpunt. De grootste van alle graafafstanden tussen de knopen van een samenhangende graaf wordt de diameter van de graaf genoemd.
De terminologie die gebruikt wordt om grafen te beschrijven, hangt af van het vakgebied. Zo wordt een kant soms een verbindingslijn genoemd, een knoop een vertex (top) of punt, en de graad van een knoop de connectiviteit. We streven ernaar om in de Network Pages consistent de woorden ‘knoop’, ‘kant’ en ‘graad’ te gebruiken.
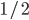 .
.
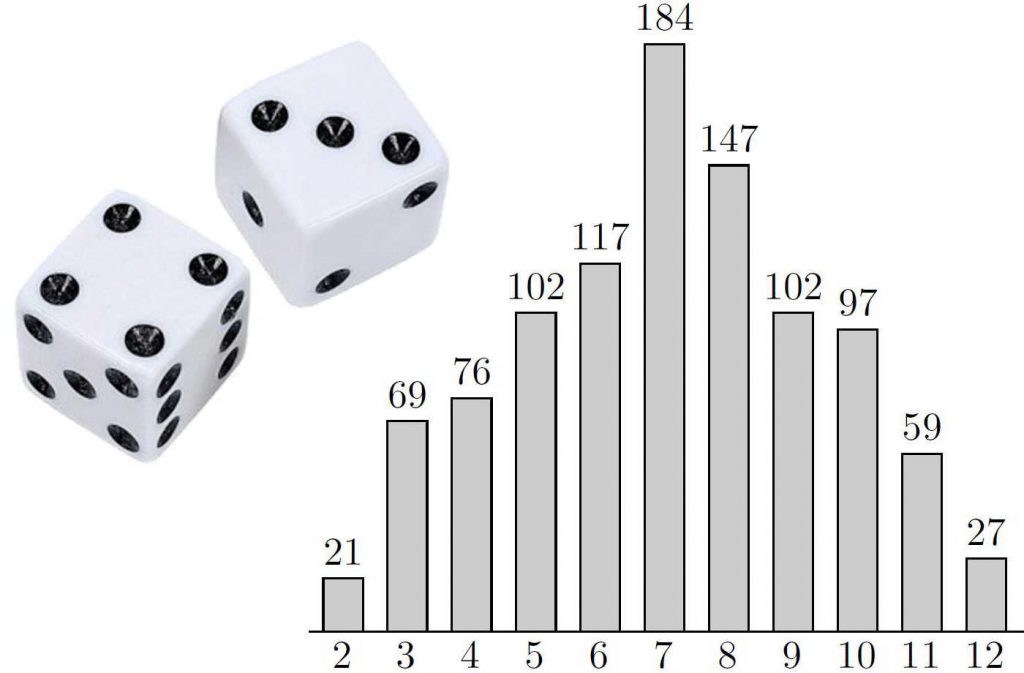
Het gooien van twee dobbelstenen. Rechts is te zien hoe vaak een bepaald totaalaantal ogen wordt verkregen als twee dobbelstenen 1000 keer worden gegooid.
Bij bordspellen vertrouwen we op willekeur. Zo gooien we bij Kolonisten van Catan twee dobbelstenen om te bepalen hoeveel kaarten iedere speler ontvangt. De uitkomst 7 is met een kans van 1 op 6 het meest waarschijnlijk; de uitkomsten 2 en 12 zijn met een kans van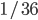 het minst waarschijnlijk. Dit verklaart waarom 6 en 8 zulke populaire getallen zijn!
Wat een waarschijnlijkheid is, kan op veel manieren geïnterpreteerd worden, en discussies hierover kunnen behoorlijk filosofisch worden. We staan hier niet stil bij deze filosofische aspecten. De waarschijnlijkheid van een gebeurtenis is het eenvoudigst te interpreteren door een experiment vele malen te herhalen, en wel op zo’n manier dat de verschillende experimenten elkaar niet beïnvloeden. In dat geval komt de waarschijnlijkheid van een bepaalde gebeurtenis overeen met het relatieve aantal keren dat de gebeurtenis optreedt tijdens een groot aantal onafhankelijke experimenten.
Prof. Remco van der Hofstad, hoogleraar kansrekening verbonden aan de technische universiteit Eindhoven, spreekt in de volgende video legt over kansrekening
het minst waarschijnlijk. Dit verklaart waarom 6 en 8 zulke populaire getallen zijn!
Wat een waarschijnlijkheid is, kan op veel manieren geïnterpreteerd worden, en discussies hierover kunnen behoorlijk filosofisch worden. We staan hier niet stil bij deze filosofische aspecten. De waarschijnlijkheid van een gebeurtenis is het eenvoudigst te interpreteren door een experiment vele malen te herhalen, en wel op zo’n manier dat de verschillende experimenten elkaar niet beïnvloeden. In dat geval komt de waarschijnlijkheid van een bepaalde gebeurtenis overeen met het relatieve aantal keren dat de gebeurtenis optreedt tijdens een groot aantal onafhankelijke experimenten.
Prof. Remco van der Hofstad, hoogleraar kansrekening verbonden aan de technische universiteit Eindhoven, spreekt in de volgende video legt over kansrekening
Mobiele telefoons, pinautomaten, moderne auto’s, televisies, e-readers: geen van deze apparaten zou werken zonder software. Het hart van software wordt gevormd door algoritmes: stap-voor-stap procedures om een bepaalde taak uit te voeren. Algoritmes kunnen uitgevoerd worden door computers maar ook door mensen.
Een voorbeeld: stel, je houdt twintig genummerde kaarten in je hand. Het is jouw taak om die op volgorde op een stapel te leggen: de kaart met het laagste nummer onderop en met het hoogste nummer bovenop. Een eenvoudig algoritme om deze taak uit te voeren ziet er als volgt uit. Loop langs alle kaarten in je hand om de kaart met het laagste nummer te vinden. Leg deze kaart neer als onderste kaart van de stapel. Loop vervolgens langs de overgebleven kaarten in je hand om de kaart met het een-na-laagste nummer vinden en leg deze op de kaart die je daarvoor had neergelegd. Herhaal deze procedure tot alle kaarten op de stapel liggen.
Om een algoritme door een computer uit te laten voeren, is het nodig om het te implementeren in computercode, bijvoorbeeld in een computertaal zoals Java of C++. Als de beschrijving van het algoritme nauwkeurig genoeg is, is het voor een ervaren programmeur niet moeilijk om het te implementeren. Dus, als je een bepaalde taak wil laten uitvoeren door een computer, ligt de uitdaging in het bedenken van een goed algoritme.
Vaak zijn er meerdere strategieën denkbaar om een bepaalde taak uit te voeren – ofwel om “een bepaald probleem op te lossen”, zoals het meestal wordt genoemd – met verschillende algoritmes tot gevolg. Deze algoritmes verschillen normaliter in hoe efficiënt ze zijn: sommige zijn snel, andere langzaam. Natuurlijk hangt de tijd die een computer daadwerkelijk nodig heeft om een probleem op te lossen af van de snelheid van de computer. Sterker nog, het hangt af van de schaal van het op te lossen probleem: duizend getallen op volgorde zetten kost minder tijd dan een miljoen getallen. Toch is het mogelijk om de efficiënties van algoritmes op wiskundige wijze met elkaar te vergelijken. Hiertoe wordt het aantal “stappen” van het algoritme geanalyseerd als functie van het aantal inputelementen.
Neem bijvoorbeeld het algoritme beschreven in Basisbegrippen – Algoritmes om genummerde kaarten op volgorde op te stapelen. Stel de input bestaat uit 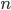 kaarten. Om de kaart met het laagste nummer te vinden, kijken we naar alle n kaarten; om de kaart met het op-een-na laagste nummer te vinden naar
kaarten. Om de kaart met het laagste nummer te vinden, kijken we naar alle n kaarten; om de kaart met het op-een-na laagste nummer te vinden naar 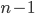 kaarten, enzovoorts. In totaal doorlopen we dus
kaarten, enzovoorts. In totaal doorlopen we dus
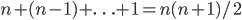
stappen. Ook al hangt het precieze aantal af van wat we als “stap” beschouwen, wat belangrijk is, is dat het aantal stappen kwadratisch toeneemt met het aantal kaarten dat gesorteerd moet worden. In technische bewoordingen is de looptijd van het algoritme 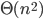 . Als de looptijd van een algoritme kwadratisch toeneemt, duurt het vier keer langer als de input verdubbelt. Een algoritme waarvan de looptijd lineair toeneemt – we schrijven: de looptijd is
. Als de looptijd van een algoritme kwadratisch toeneemt, duurt het vier keer langer als de input verdubbelt. Een algoritme waarvan de looptijd lineair toeneemt – we schrijven: de looptijd is 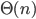 – kost maar twee keer zoveel tijd als de input verdubbelt. Lineaire-looptijdalgoritmes zijn dus veel sneller dan kwadratische-looptijdalgoritmes bij grote inputs.
– kost maar twee keer zoveel tijd als de input verdubbelt. Lineaire-looptijdalgoritmes zijn dus veel sneller dan kwadratische-looptijdalgoritmes bij grote inputs.
Een belangrijk onderscheid tussen algoritmes is of hun looptijd polynomiaal toeneemt met de inputschaal 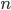 , bijvoorbeeld als
, bijvoorbeeld als 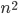 of
of  , of exponentieel, als
, of exponentieel, als 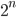 of
of 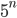 . De looptijd van laatstgenoemde type algoritmes groeit zo snel dat ze in feite onbruikbaar zijn tenzij de inputschaal zeer klein is. Stel, bijvoorbeeld, dat we een algoritme hebben dat
. De looptijd van laatstgenoemde type algoritmes groeit zo snel dat ze in feite onbruikbaar zijn tenzij de inputschaal zeer klein is. Stel, bijvoorbeeld, dat we een algoritme hebben dat 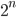 stappen uitvoert bij een inputschaal
stappen uitvoert bij een inputschaal 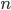 , en dat we een computer hebben die 1 miljard stappen per seconde kan uitvoeren. In dat geval kost het het algoritme ongeveer 1 seconde bij een input van 30. Maar als de inputschaal 50 is, zou het 36 jaar kosten… Het helpt niet veel om een snellere computer te kopen. In plaats daarvan zou je moeten proberen om een efficiënter algoritme te bedenken. Het zoeken naar het efficiëntste algoritme voor een bepaald rekenprobleem is een levendige en belangrijke tak van sport binnen de theoretische informatica.
, en dat we een computer hebben die 1 miljard stappen per seconde kan uitvoeren. In dat geval kost het het algoritme ongeveer 1 seconde bij een input van 30. Maar als de inputschaal 50 is, zou het 36 jaar kosten… Het helpt niet veel om een snellere computer te kopen. In plaats daarvan zou je moeten proberen om een efficiënter algoritme te bedenken. Het zoeken naar het efficiëntste algoritme voor een bepaald rekenprobleem is een levendige en belangrijke tak van sport binnen de theoretische informatica.
Willekeurige grafen zijn grafen die opgesteld zijn op basis op van probabilistische regels. Zo worden de kanten en knopen van de graaf bepaald door een kansexperiment uit te voeren. Het idee hierachter kan zijn dat mensen elkaar op onvoorspelbare wijze kunnen ontmoeten, en dus dat de precieze onderlinge verbindingen gezien kunnen worden als de uitkomst van een kansexperiment.
In de Network Pages beschrijven we enkele willekeurige graaf modellen die gebruikt zijn om alledaagse netwerken te beschrijven, zoals de Erdős-Rényi willekeurige graaf, het configuratiemodel en preferential attachment modellen.
