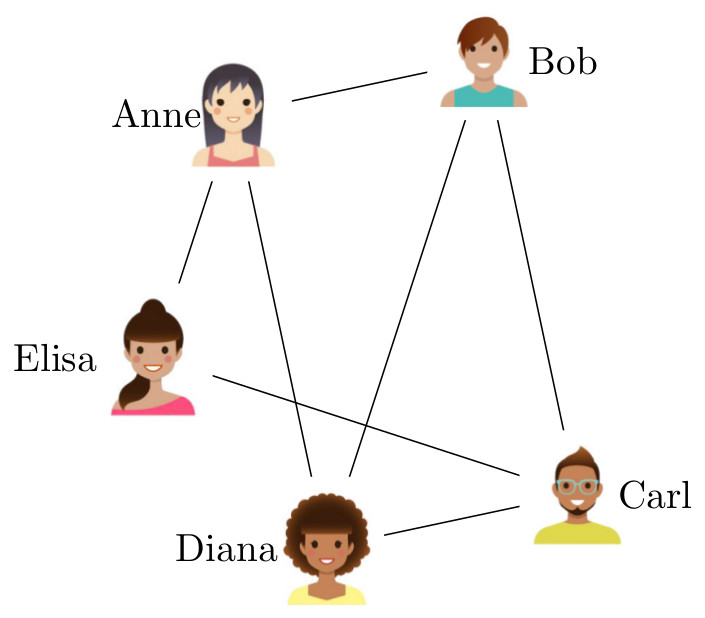
Zoals eerder uitgelegd, bestaat een netwerk uit objecten die onderling verbonden zijn. Wiskundigen noemen zo'n netwerk een graaf, en de objecten knopen (of vertices), en de verbindingen kanten. Als we bijvoorbeeld een sociaal netwerk van een groep mensen weergeven als een graaf, dan zijn de knopen de mensen waar het om gaat, en beschrijven de kanten hun onderlinge relaties. Dus, als Anne en Bob twee vrienden zijn in het sociale netwerk, dan bevat de graaf een "Anne"-knoop en een "Bob"-knoop met een kant ertussen.
In treinnetwerken staan de knopen voor de treinstations en de kanten voor de spoorlijnen waarmee ze onderling verbonden zijn. Uiteraard zijn we soms ook geïnteresseerd in de eigenschappen van de objecten en hun verbindingen, maar daar gaan we nu nog niet op in.
We noemen nog enkele voorbeelden van netwerken. In het netwerk van Facebookvriendschappen staan de knopen voor Facebookgebruikers en trekken we kanten tussen Facebookvrienden. In het netwerk van acteurs die opgenomen zijn in de Internet Movie DataBase (IMDB) staan de knopen voor de acteurs en tekenen we kanten tussen iedere twee acteurs die samengewerkt hebben in een film. In een graaf van het internet kunnen de knopen staan voor routers en de kanten voor fysieke kabels die routers met elkaar verbinden. In het World-Wide Web staan de knopen voor webpagina’s en de kanten voor de hyperlinks waarmee ze verbonden zijn. Soms kunnen datasets door middel van meerdere netwerken weergegeven worden. In het voorbeeld van het IMDB kunnen we ook de films als knopen beschouwen en een kant tekenen tussen twee films als een acteur in beide heeft gespeeld. Verschillende netwerkweergaves kunnen inzicht bieden in de verschillende eigenschappen van datasets.
In veel netwerken hebben de verbindingen een richting die van belang is. In een wegennetwerk bijvoorbeeld is het best belangrijk om de rijrichting van het eenrichtingsverkeer te weten!
Laten we nu enkele basisbegrippen uit de grafentheorie bespreken. De graad van een knoop is het aantal verbindingen dat het heeft, of, in andere woorden, het aantal kanten waar het deel van uit maakt. Een graaf wordt samenhangend genoemd als het mogelijk is om tussen ieder tweetal knopen te bewegen door van knoop naar knoop te springen. De graafafstand tussen twee knopen is het kleinste aantal kanten tussen die knopen, of het kleinste aantal stappen dat genomen moet worden van start- naar eindpunt. De grootste van alle graafafstanden tussen de knopen van een samenhangende graaf wordt de diameter van de graaf genoemd.
De terminologie die gebruikt wordt om grafen te beschrijven, hangt af van het vakgebied. Zo wordt een kant soms een verbindingslijn genoemd, een knoop een vertex (top) of punt, en de graad van een knoop de connectiviteit. We streven ernaar om in de Network Pages consistent de woorden 'knoop', 'kant' en 'graad' te gebruiken.
