Heeft u zich ooit eens afgevraagd hoe u wiskunde interessant kunt maken in het dagelijkse leven van leerlingen?
Welke wiskundedocent is nog niet geconfronteerd met de vraag "Waarom leren we wiskunde?" In dit artikel zullen verschillende benaderingen worden besproken waarmee docenten grafentheorie kunnen introduceren in hun lessen. Grafentheorie wordt specifiek gekozen vanwege haar significante rol binnen de wiskunde en de diverse praktische toepassingen in het dagelijks leven. Door dit onderwerp te belichten, kunnen we onze leerlingen laten inzien waarom wiskunde van essentieel belang is. We gaan ervan uit dat de leerlingen reeds bekend zijn met formules en bedreven zijn in rekenen.
Wat is precies grafentheorie? Voordat we de definitie bespreken, zullen we beginnen met enkele voorbeelden: We denken aan het netwerk van treinen, het netwerk van snelwegen, maar zelfs je eigen Google Maps die de snelste route berekent om van je huis naar je werk te komen.
We zijn nu klaar om de technische details te bespreken.
Het kortste pad algoritme
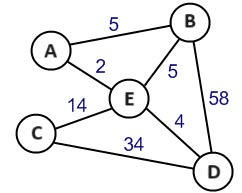
Grafentheorie is de theorie die werkt met punten (de steden) en lijnen (routes) en hun onderlinge relatie laat zien. Ter illustratie kijken we naar figuur 1. Dit is een voorbeeld van een vrij eenvoudige graaf. We laten de getallen de afstand tussen de drie steden, A, B, C, D, E, voorstellen. Om de kortste route van stad A naar C te vinden, kun je gewoon de afstanden van alle routes berekenen.
Figuur 1: Het spoorwegen netwerk van de Randstad in Nederland.
Maar als we naar nog meer steden en routes tussen hen kijken, krijgen we iets als figuur 2, waar de complexiteit toeneemt. Als we alle afstanden afzonderlijk zouden berekenen, zouden we hopeloos verdwalen. Door dit te behandelen als een grafentheoretisch probleem, kunnen wij een vrij eenvoudig algoritme gebruiken om dit probleem op te lossen: het algoritme van Dijkstra. (Meer informatie en materiaal voor in de klas over Dijkstra's algoritmes in het algemeen en het algoritme van Dijkstra is te vinden in het boekje van de jaarlijkse masterclass NETWORKS goes to school).
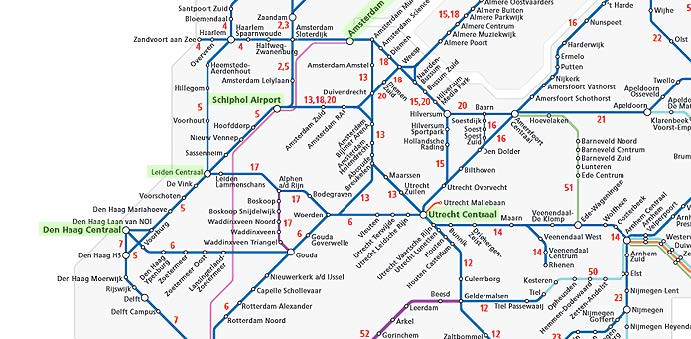
Figuur 2: Het spoorwegen netwerk van de Randstad in Nederland.
Dit is een voorbeeld van hoe men grafentheorie in hun lessen zou kunnen implementeren. Maar het potentieel van grafentheorie gaat verder dan alleen route-optimalisatie. Laten we eens kijken naar een ander onderwerp in de grafentheorie: het kleuren van grafen.
Het kleuren van grafen
Waarom zou men geïnteresseerd zijn in het inkleuren van grafen en wat bedoelen we daar precies mee? Laten we eerst de reden bespreken: Op kaarten van de wereld worden landen vaak weergegeven met verschillende kleuren om ze te onderscheiden. Maar wat als we deze kleuren zo efficiënt mogelijk willen gebruiken? Hier komt grafentheorie om de hoek kijken. Binnen grafentheorie onderzoeken we de minimale hoeveelheid kleuren die nodig is om grafen in te kleuren; dit wordt het chromatische getal genoemd. Het berekenen van dit chromatische getal is vaak een uitdagend probleem. Dit onderwerp is zo interessant en spannend dat we een hele lijst met artikelen hebben hierover.
Niettemin vormt het een boeiende uitdaging die de verbeelding van studenten kan prikkelen. We kunnen dit concept toepassen op eenvoudige grafen, zoals te zien is in figuur 1 (probeer dit zelf te doen). Daaruit blijkt dat we minimaal drie kleuren nodig hebben.
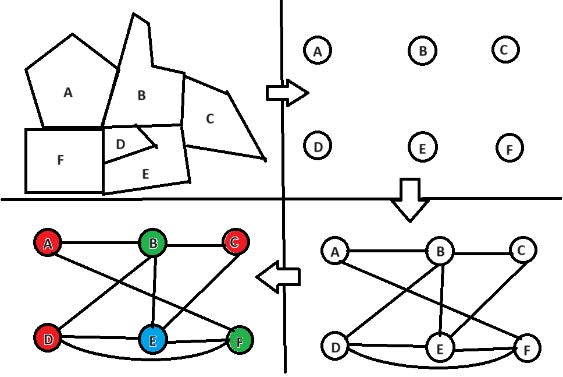
Figuur 3: een voorbeeld hoe we een kaart kunnen kleuren door middel van grafentheorie.
Hoe kunnen we echter van kaarten naar grafen gaan? We identificeren eerst de landen met punten, en als de landen een grens delen, worden ze verbonden door een lijn. Vervolgens kunnen we de punten van de graaf inkleuren. Daarna kleuren we de landen met de overeenkomstige kleur van het punt, waardoor we iets krijgen zoals figuur 3.
We kunnen zien dat we grafentheoretische problemen kunnen gebruiken om studenten te laten zien dat niet alle onderwerpen in de wiskunde het oplossen van saaie vergelijkingen zijn. In feite kunnen ze wegen zijn naar het begrijpen en vormgeven van de wereld om ons heen. En dat sommige delen van de wiskunde zelfs toepasbaar zijn op hun dagelijks leven. Dus in plaats van  Waarom leren we dit?
Waarom leren we dit? , zullen we hopelijk de vraag krijgen:
, zullen we hopelijk de vraag krijgen:  Is er meer te leren?
Is er meer te leren? .
.
Wilt u een les ontwerpen over grafentheorie, netwerken, of algoritmes? Dan kunt u misschien inspiratie opdoen van de boekjes die waren gemaakt voor de masterclass NETWORKS goes to school! Voel vrij om deze te gebruiken in uw lessen!