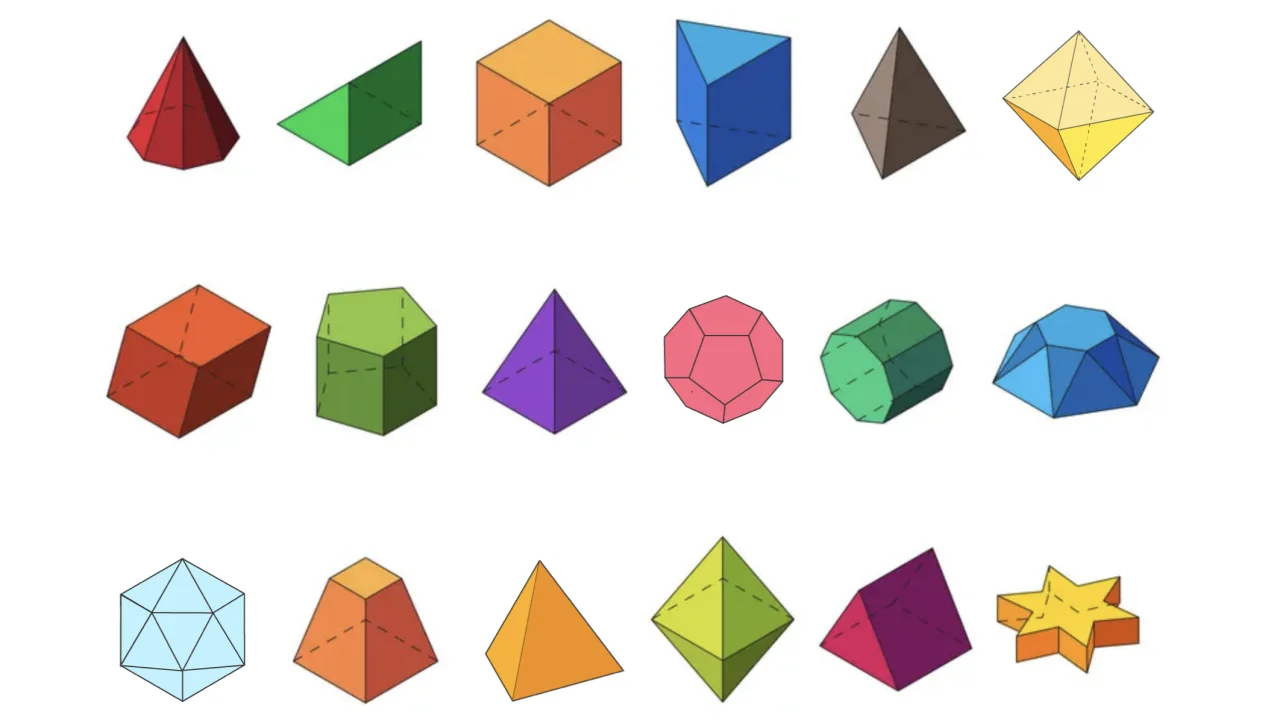
De Stelling van Descartes - The Network Pages

Deze lesmodule behandelt twee stellingen uit de meetkunde: de stelling van Euler voor veelvlakken, en de stelling van Descartes. Opvallend genoeg spelen grafen een cruciale rol in het bewijs van de eerste stelling!

Wiskundestudenten Koen van Baar, Wiebe Hoving, en Hamza Yusuf van de Universiteit van Amsterdam hebben twee lesboekjes geschreven voor leerlingen aan het einde van de onderbouw of begin van de bovenbouw HAVO/VWO. Het eerste boekje bespreekt de formule van Euler voor veelvlakken, terwijl het tweede boekje gaat een stap verder en behandelt het hoofdonderwerp van deze lesmodule, de stelling van Descartes.

De twee lesboekjes zijn hier te vinden. De boekjes zijn bedoeld voor leerlingen die dit onderwerp interessant vinden, maar ook voor docenten die een les willen geven over meetkunde in drie dimensies.

Doelgroep: leerlingen aan het einde van de onderbouw of begin van de bovenbouw HAVO/VWO.

Evaluatie: Deze lesmodule is voorgelegd aan en geëvalueerd met wiskunde docenten tijdens de NWD 2023.

De Stelling van Descartes: een minder bekend juweeltje

Als we meetkundeles krijgen dan ligt de focus vooral op meetkunde in twee dimensies. We leren dat de som van de hoeken van een driehoek altijd gelijk is aan 180 graden, maar ook hoe we de som van alle hoeken in een regelmatige veelhoek kunnen bepalen. We werken tevens minder met objecten in drie dimensies. Een resultaat dat soms wordt behandeld op school is de formule van Euler voor convexe veelvlakken, namelijk dat $H-R+F = 2$ , waarbij $H$ staat voor het aantal hoekpunten, $R$ voor het aantal ribben, en $F$ voor het aantal zijvlakken (facetten).

De stelling van Descartes is een juweeltje uit de meetkunde die minder bekend is, het gaat over de hoeken van veelvlakken en luidt als volgt:

Stelling van Descartes
Als we de defecten van hoeken van verschillende veelvlakken bij elkaar optellen, krijgen we altijd 720 graden.

Dit is een verrassend resultaat. Het blijkt dat voor elk veelvlak dat convex is, het totale defect van de hoeken gelijk is aan 720 graden. Convex betekent dat een lijn tussen twee punten op het veelvlak altijd in het veelvlak zelf zit. Dit houdt in dat het veelvlak geen indeukingen of gaten mag hebben. Het feit dat elk convex veelvlak een totaal hoektekort van 720 graden heeft, wordt ook wel de stelling van Descartes genoemd. In de boekjes worden alle deze concepten verder toegelicht. Met behulp van de stappen en de opgaven in de boekjes kunnen de leerlingen de stelling zelf bewijzen.

Leerdoelen boekjes

Bij het afronden van deze lesmodule weten de leerlingen:

wat een graaf is
wat een samenhangende graaf en planaire graaf zijn;
wat de formule van Euler voor veelvlakken zegt. Bovendien ze kunnen de formule in de juiste gevallen toepassen om logische conclusies te trekken;
hoe ze een schlegeldiagram moeten tekenen bij relatief simpele veelvlakken;
hoe de formule van Euler voor veelvlakken bewezen wordt;
hoe ze het hoekdefect van een hoekpunt en het totale hoekdefect van een veelvlak kunnen berekenen;
wat de stelling van Descartes zegt;
hoe het bewijs van de stelling van Descartes volgt uit de formule van Euler voor veelvlakken.

In het eerste boekje richten we ons voornamelijk op leerdoelen 1-5. We beginnen met een introductie van het concept van een graaf. Hierbij leggen we ook uit wat een samenhangende graaf en een planaire graaf zijn, aangezien deze begrippen essentieel zijn voor het begrijpen van de stelling van Descartes. De leerlingen beantwoorden enkele vragen over deze soorten grafen om het begrip verder te verdiepen.

Vervolgens laten we de leerlingen een vermoeden formuleren over het verband tussen het aantal punten, lijnen en facetten in een graaf. Daarna introduceren we de formule van Euler en laten we de leerlingen Schlegeldiagrammen maken van verschillende veelvlakken. Tot slot bewijzen we, aan de hand van eenvoudige voorbeelden zoals een kubus en een tetraëder, de formule van Euler voor veelvlakken.

In het tweede boekje behandelen we leerdoelen 6, 7 en 8, met de focus op de stelling van Descartes. Eerst leggen we uit wat het hoektekort is bij tweedimensionale figuren. Daarna laten we de leerlingen zelf werken met het hoektekort in drie dimensies, waarbij we ook de stelling van Descartes introduceren. Stap voor stap begeleiden we de leerlingen bij het bewijzen van deze stelling.

In beide lesboekjes moedigen we de leerlingen aan om zelf verbanden te ontdekken. In het boekje over de formule van Euler voor veelvlakken laten we ze zelfstandig de waarde van $H-R+F$ berekenen voor verschillende veelvlakken. Zo ontdekken ze zelf dat de uitkomst telkens 2 is. In het boekje over de stelling van Descartes berekenen de leerlingen het totale hoektekort van een veelvlak, en ontdekken ze dat dit steeds 720 graden is. Met deze aanpak willen we de nieuwsgierigheid van de leerlingen prikkelen en verwachten we dat ze de stof beter begrijpen en onthouden.