De meeste mensen kennen het spelletje ‘Set’ wel, waarbij een serie kaarten wordt neergelegd en de spelers zo snel mogelijk moeten uitzoeken of er een drietal is waarbij alle kenmerken ofwel gelijk ofwel verschillend zijn. Dat heet dan een set. Het spel draait om inzicht en snel deduceren.
Zoals het spel nu bestaat, zijn er vier kenmerken (kleur, vorm, aantal en vulling), met ieder drie opties. Ik heb in mijn profielwerkstuk een voor ieder kenmerk een optie toegevoegd (dus een extra kleur, vorm, aantal en vulling). Een set bestaat dan uit vier kaarten. Dit spel bestond nog niet, dus ik heb het laten maken. Ik heb in mijn profielwerkstuk onderzocht welke wiskundige principes op beide spellen van toepassing zijn. De hoofdvraag van mijn onderzoek was als volgt:
Wat zijn de wiskundige consequenties van het vermeerderen van het aantal opties van de bestaande kenmerken van het spel ‘Set’?
Een voorbeeld van een set: de kleur, vorm en vulling van de kaarten zijn verschillend terwijl het aantal bij alle drie hetzelfde is.
De eerste en meest praktische consequentie was de speelbaarheid. Waar het spel met drie opties leuk en speelbaar is, is het spel met vier opties onmogelijk en niet meer leuk. Niet alleen duurt het veel te lang (de stapel kaartjes is meer dan drie keer zo groot geworden), ook bleek het niet eenvoudig om een set van vier kaarten te vinden. Het meest lastig is dat in het normale Set-spel bij iedere twee kaarten slechts één derde kaart past, terwijl bij de uitgebreide versie nog meerdere derde kaarten passen (en de meeste uiteraard niet), waarna nog één vierde kaart past, die meestal niet in het veld ligt. Deze factoren zorgen ervoor dat het spel niet meer als spel te spelen is.
Gelukkig heb ik het spel niet laten maken om te spelen, maar om er onderzoek naar te doen. Mijn profielwerkstuk is opgedeeld in de volgende drie deelvragen:
Hoe kunnen de spellen wiskundig in beeld worden gebracht?
Hoeveel kaarten kunnen er maximaal in het veld zonder set?
Wat is het totaal aantal sets in beide spellen?
Ik heb de antwoorden van deze deelvragen bij beide spellen gezocht. Daarna heb ik de antwoorden van het originele spel en van mijn uitbreding vergeleken. In dit artikel behandel ik alleen de derde deelvraag, het totaal aantal sets. Als je ook geïnteresseerd bent in de rest kun je het hele profielwerkstuk binnenkort lezen op de website van Pythagoras.
Het totaal aantal sets berekenen in het spel met drie opties is vrij eenvoudig. Je kunt namelijk gebruikmaken van het feit dat je twee willekeurige kaarten kunt pakken waar dan één derde kaart bij hoort. Er zitten in totaal kaarten in het spel, dus het aantal sets is . Hierin zit een behoorlijke overlap, omdat de mogelijkheden (weergegeven in getallen) 123, 132, 213, 231, 321 en 312 allemaal geteld worden, terwijl het maar één set is. Omdat een set uit drie kaarten bestaat, zijn alle combinaties keer geteld. Om het echte aantal sets te berekenen, moet de uitkomst (6480 sets) worden gedeeld door het aantal dubbeltellingen. Het totaal aantal sets is dus .
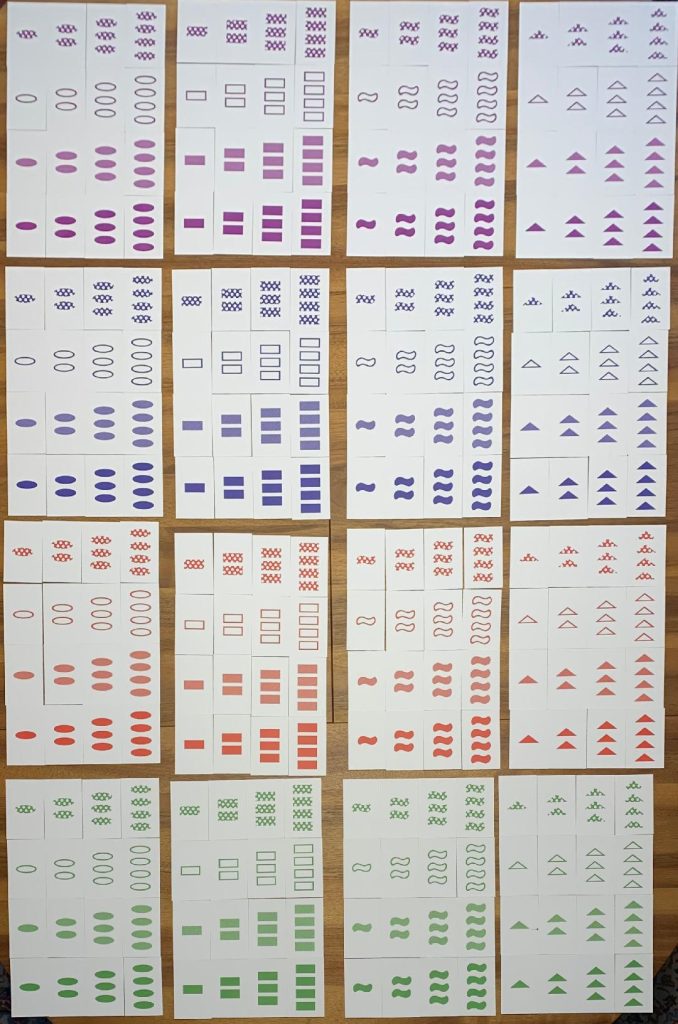
De uitbreiding van het spel Set dat Femke heeft laten maken.
Deze “simpele” manier van berekenen vervalt helaas als er vier opties zijn. Dat komt doordat het aantal mogelijke derde kaarten afhankelijk is van hoe verschillend de eerste twee kaarten zijn. Als de eerste twee kaarten maar op één kenmerk van elkaar verschillen, is er nog maar één set mee te maken, maar als de eerste twee kaarten helemaal anders zijn, zijn er (in het spel met vier opties) nog acht verschillende sets mee te maken. Omdat iedere soort set dus een andere berekening nodig heeft, moet een onderscheid worden gemaakt tussen vier groepen: sets waarbij alle kenmerken anders zijn, sets waarbij één kenmerk hetzelfde is, sets waarbij twee kenmerken hetzelfde zijn en sets waarbij drie kenmerken hetzelfde zijn. Voor alle groepen moet een aparte berekening gemaakt worden, waarna die bij elkaar opgeteld moeten worden. Hieronder staan de uitwerkingen:
Sets waarbij alle kenmerken anders zijn: voor de eerste kaart kun je 256 kaarten pakken (het aantal kaarten in het spel), en voor de tweede kaart alleen maar de kaarten die helemaal anders zijn. Dat zijn er 81 (je mist één optie bij alle kenmerken, dus je houdt een basisspel over, met drie opties bij ieder kenmerk). Voor de derde kaart heb je een kaart nodig die helemaal anders is dan de eerste twee. Daarvoor zijn 16 kaarten mogelijk (een spel met twee opties). Voor de laatste kaart is nog maar één mogelijkheid. De berekening wordt daarmee: \begin{equation} 256 * 81 * 16 * 1 = 331.776 \text{ sets.}\end{equation}
Sets waarbij één kenmerk hetzelfde is: voor de eerste kaart kan je nog steeds 256 kaarten pakken, en voor de tweede kaart moet je één kenmerk hetzelfde houden. Stel je hebt de eerste kaart helemaal linksboven gepakt (een enkele paarse gestipte ovaal) en je wil het kenmerk kleur hetzelfde houden. De kaarten zijn neergelegd in zestientallen, in vier rijen en vier kolommen. Om de kleur hetzelfde te houden moet je kaarten uit de eerste rij kiezen. Maar alle kaarten in het eerste zestiental hebben dezelfde vorm. De andere drie zestientallen bevatten wel kaarten, elk negen:
Dat zijn dus mogelijke kaarten. De derde kaart moet wederom paars zijn. De andere drie kenmerken moeten anders zijn dan bij de eerste twee kaarten. Voor elk van deze drie kenmerken heb je nu dus twee opties. Voor de derde kaart heb je dus opties. Voor de laatste kaart is nog één mogelijkheid.
In het voorbeeld kozen we om een set te bouwen waarbij de kleur hetzelfde bleef. Maar we hadden ook een ander kenmerk kunnen kiezen. We moeten daarom ook vermenigvuldigen met 4 voor het totaal aantal sets. Het totaal aantal sets wordt daarmee: \begin{equation} 4 * 256 * 27 * 8 *1 = 221.184 \text{ sets.}\end{equation}
Puzzel: ga nu zelf na dat er voor sets waarbij twee kenmerken hetzelfde zijn in totaal 55.296 sets zijn en voor drie kenmerken hetzelfde 6.144 sets.
Om het totaal aantal mogelijke sets in de verzameling te berekenen, moeten de vier verschillende aantallen bij elkaar worden opgeteld. De berekening ziet er dan zo uit: \begin{equation} 331776 + 221184 + 55296 + 6144 = 614.400 \text{ sets.}\end{equation}
Maar ook hier zitten dubbeltellingen in. Omdat een set uit vier kaarten bestaat, is iedere set precies keer geteld, dus 614400 moet door dat getal gedeeld worden. Het totaal aantal sets is dan: \begin{equation} 614400 / 4! = 25.600 \text{ sets.}\end{equation}
Oké, we weten nu hoeveel sets er in het spel met vier opties zitten, maar hoe zit het met meer dan vier opties? Laten we proberen een algemene formule te maken waarmee je het aantal sets kunt berekenen voor ieder aantal opties.
Voor deze berekening verdelen we de sets weer in vier groepen, net als bij de berekening van vier opties. We noemen het aantal opties en het aantal sets . Een set bestaat dan uit kaarten, net als dat een set bij drie opties uit drie kaarten bestaat, en bij vier opties uit vier kaarten.
Sets waarbij alle kenmerken anders zijn: voor de eerste kaart zijn er mogelijkheden (het aantal kaarten). Omdat de tweede kaart volledig anders moet zijn, valt er bij ieder kenmerk een optie af. Als je al deze kaarten weghaalt, krijg je hetzelfde spel met één optie minder. Voor de tweede kaart zijn er dus nog mogelijkheden over. Als je dezelfde denkstappen toepast voor de derde kaart, kom je erachter dat er voor de derde kaart mogelijkheden zijn .Dit patroon gaat door tot en met de laatste kaart. Een set bestaat uit kaarten, dus krijg je een product van termen. De laatste term is . Dit schrijf je als volgt op: \begin{equation} p^4 * (p-1)^4 * (p-2)^4 *\cdots* 1^4. \end{equation}
Omdat al deze termen tot de vierde macht staan, kun je de vierde macht buiten de haakjes zetten, zoals hieronder: \begin{equation} \left( p * (p-1) * (p-2) * \cdots * 1\right)^4. \end{equation}
Dit lijkt een kleine verandering, maar het stuk tussen haakjes is hetzelfde als \(p\). Daarmee kan de berekening versimpeld worden tot.
Sets waarbij één kenmerk hetzelfde is: Voor de eerste kaart zijn er weer mogelijkheden. Ook zijn er vier mogelijke kenmerken die we hetzelfde kunnen houden. Voor de tweede kaart moeten drie kenmerken anders zijn dan de eerste kaart. Voor elk van de drie kenmerken zijn er nog opties, omdat de opties van de eerste kaart niet meer gekozen mogen worden. Dus voor de tweede kaart zijn er opties. Voor de derde kaart zijn er per kenmerk nog opties en dus zijn er opties. Dit gaat zo door tot en met de laatste kaart. Het totaal aantal sets in deze groep is dus \begin{equation} 4*p^4 * (p-1)^3 *(p-2)^3 * \cdots * 2^3. \end{equation}
Nu we hebben bekeken hoe de berekening de maken is, is het aan jou om de berekeningen voor sets waarbij twee en drie kenmerken hetzelfde zijn te maken.
Als je de berekeningen goed hebt gevonden, kom je erop uit dat het totaal aantal sets het volgende is: \begin{equation} 1p^0 * p!^4 + 4p^1 * p!^3 + 6p^2 * p!^2 + 4p^3 * p!^1.\end{equation}
Als je wiskunde A of D hebt (gehad), ben je waarschijnlijk wel bekend met de driehoek van Pascal. Dat is een driehoek met getallen, die op veel manieren wiskundige patronen heeft. Je kunt deze driehoek ook gebruiken om snel haakjes met hogere machten uit te rekenen. Als je bijvoorbeeld een vierde macht uit wil rekenen, krijg je het volgende: \begin{equation}(a+b)^4 = 1a^4b^0 + 4a^3b^1 + 6a^2b^2 + 4a^1b^3 + 1a^0b^4\end{equation}
Deze uitwerking lijkt best wel op de formule die we hebben gemaakt. Dan zou het volgende gelden: en . Dit klopt bijna helemaal, er ontbreekt alleen een term , want er is geen . Als we de formule dus zouden willen omschrijven naar haakjes, zouden we die term er dus nog af moeten halen. Ook hebben we nog sets dubbel geteld in deze formule, wat betekent dat we het totaal nog moeten delen door . De uiteindelijke formule wordt dan:
\begin{equation} T = \frac{(p+p!)^4 - p^4}{p!}. \end{equation}
In mijn profielwerkstuk heb ik dus gekeken naar wat er gebeurt als je het bekende spel Set uitbreidt van drie naar vier opties per kenmerk. Waar het originele spel goed speelbaar is en overzichtelijk blijft, blijkt het uitgebreide spel veel complexer, zowel in praktische speelbaarheid als in wiskundige structuur.
Op tijd komen is niet moeilijk, mits je op tijd vertrekt en de snelste route neemt. Maar hoe vind je de snelste route als er sprake is van verkeer? Dylan en Tobias schreven hier een profielwerkstuk over en wonnen er de Pythagorasprijs mee!
Deze lesmodule, geschreven voor leerlingen aan het einde van de onderbouw of begin van de bovenbouw HAVO/VWO, behandelt twee stellingen uit de meetkunde: de stelling van Euler voor veelvlakken, en de stelling van Descartes.
Er zijn verschillende parameters die bepalen of een video viraal gaat of niet. De inhoud speelt uiteraard een rol, maar wie de video uploadt, is ook belangrijk. Wat hebben netwerken te maken met een video die viraal gaat?
Het doel van dit project was om middelbare scholieren (5 VWO wiskunde D) in contact te brengen met de intrigerende wiskunde achter kunstmatige intelligentie, en hen te inspireren om deze wondere wereld te verkennen.
kaarten in het spel, dus het aantal sets is 
. Hierin zit een behoorlijke overlap, omdat de mogelijkheden (weergegeven in getallen) 123, 132, 213, 231, 321 en 312 allemaal geteld worden, terwijl het maar één set is. Omdat een set uit drie kaarten bestaat, zijn alle combinaties 
keer geteld. Om het echte aantal sets te berekenen, moet de uitkomst (6480 sets) worden gedeeld door het aantal dubbeltellingen. Het totaal aantal sets is dus 
.
mogelijke kaarten. De derde kaart moet wederom paars zijn. De andere drie kenmerken moeten anders zijn dan bij de eerste twee kaarten. Voor elk van deze drie kenmerken heb je nu dus twee opties. Voor de derde kaart heb je dus 
opties. Voor de laatste kaart is nog één mogelijkheid.
keer geteld, dus 614400 moet door dat getal gedeeld worden. Het totaal aantal sets is dan: \begin{equation} 614400 / 4! = 25.600 \text{ sets.}\end{equation}
en het aantal sets 
. Een set bestaat dan uit 
mogelijkheden (het aantal kaarten). Omdat de tweede kaart volledig anders moet zijn, valt er bij ieder kenmerk een optie af. Als je al deze kaarten weghaalt, krijg je hetzelfde spel met één optie minder. Voor de tweede kaart zijn er dus nog 
mogelijkheden over. Als je dezelfde denkstappen toepast voor de derde kaart, kom je erachter dat er voor de derde kaart 
mogelijkheden zijn .Dit patroon gaat door tot en met de laatste kaart. Een set bestaat uit 
. Dit schrijf je als volgt op: \begin{equation} p^4 * (p-1)^4 * (p-2)^4 *\cdots* 1^4. \end{equation}
.
opties, omdat de opties van de eerste kaart niet meer gekozen mogen worden. Dus voor de tweede kaart zijn er 
opties. Voor de derde kaart zijn er per kenmerk nog 
opties en dus zijn er 
opties. Dit gaat zo door tot en met de laatste kaart. Het totaal aantal sets in deze groep is dus \begin{equation} 4*p^4 * (p-1)^3 *(p-2)^3 * \cdots * 2^3. \end{equation}
en 
. Dit klopt bijna helemaal, er ontbreekt alleen een term 
, want er is geen 
. De uiteindelijke formule wordt dan:
