Nooit meer een briefje halen: op tijd komen met wiskunde

Tijdens het Nederlands Mathematisch Congres 2025 ontvingen Dylan en Tobias de Pythagoras Profielwerkstukprijs voor hun uitstekende profielwerkstuk. In 2024 namen zij deel aan de masterclass NETWORKS goes to school, waar zij inspiratie opdeden voor hun werk.

“Please get a note…” zei de docent Engels altijd wanneer je, ook maar een seconde na het begin van de les, het lokaal binnenliep. En zo was je alweer vroeg in de ochtenddauw fietsend onderweg om je om kwart over acht op school te melden. Niet alleen frustrerend voor jou, maar ook voor de leraar, wiens les wordt verstoord door de laatkomer. Op tijd komen is niet moeilijk, mits je op tijd vertrekt en de snelste route neemt. Maar wat is de snelste route eigenlijk?

Beeld je in: de bel gaat en je moet vanaf de aula naar de wiskundeles. Je kent de weg, al heb je nooit gemeten of dat ook echt de kortste route is. Je stopt je broodtrommel in je tas en start met lopen. Voor je het weet sta je vast op de trap, de brugklassers die met te volgeladen tassen onnodig veel ruimte innemen helpen niet mee bij deze opstopping. Had je toch een stukje om moeten lopen om de file te vermijden? Misschien toch via de glijbaan moeten gaan (ja, onze school heeft er een)? Het kortste pad is in dit geval niet het snelste pad! Voor ons profielwerkstuk hebben we een website gemaakt die het vinden van de beste route op school makkelijker maakt. En achter de schermen? Daar zit een heleboel leuke wiskunde!

De glijbaan in het Hyperion Lyceum. Om de snelheid van de glijbaan te bepalen zijn we er maar liefst 8 keer afgegaan!

Het kortste pad

Laten we simpel beginnen. Wellicht zijn er twee routes van de aula naar het wiskundelokaal die ongeveer even lang lijken. Welke is eigenlijk de kortste? We kunnen natuurlijk meten hoe lang beide routes duren. Maar datzelfde doen voor alle duizenden mogelijke routes in een schoolgebouw zou jaren duren. Met interesse in wiskunde en een vleugje luiheid kan een veel betere oplossing gevonden worden.

In plaats van alle gehele routes op te meten breken we alles op in route-stukjes. Zo hoeven we de lengte van een gang maar één keer te meten en kunnen we dit voor alle routes, die door deze gang gaan, gebruiken.

We modelleren de infrastructuur van de school als een graaf. Lees in dit artikel meer over grafentheorie. In deze graaf zijn alle gangen, trappen en andere mogelijke route-stukjes weergegeven als een lijn (genaamd zijde). De relevante locaties zoals lokalen en wc’s, samen met kruispunten van de route-stukjes, worden weergegeven als genummerde punten (genaamd vertices). Hieronder is de plattegrond van de eerste verdieping met een deel van de getekende graaf erop. De volledige graaf strekt over het gehele schoolgebouw, dat zijn maar liefst 6(!) verdiepingen.

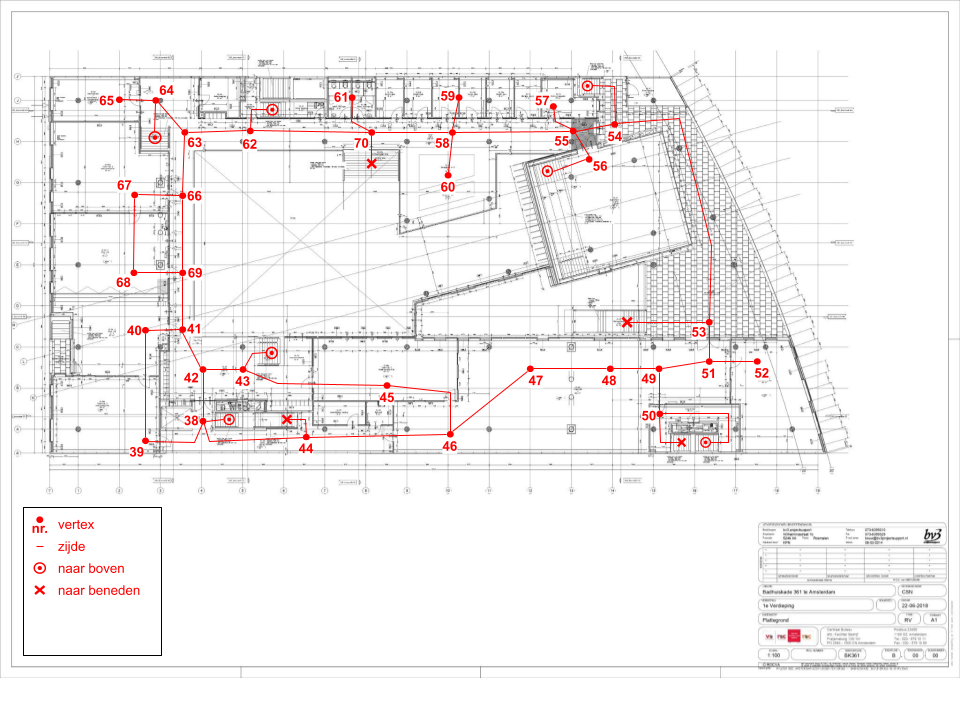
Plattegrond van de eerste verdieping. De graaf is weergegeven in het rood.

Nu we het gebouw hebben opgebroken in een overzichtelijk netwerk, kunnen we elke individuele zijde gaan meten. Dat kan natuurlijk door alles te lopen en te timen. Gelukkig kunnen we ook gewoon de afstand via de plattegrond opmeten en omzetten (met een gemiddelde loopsnelheid van 1,34 m/s) naar een looptijd. Hier kan zo nodig tijd aan toegevoegd worden voor traplopen of deuren openen. Door deze metingen toe te voegen aan de zijden van de graaf, krijgen we een gewogen graaf.

Een voorbeeld van een gewogen graaf. Een gewogen graaf is een netwerk van vertices (punten) en zijden (lijnen) waarbij de zijden een gewicht krijgen. Denk hierbij aan een afstand of een tijd; dit laatste is bij ons het geval.

Deze graaf vormt het grondwerk waarop Dijkstra’s kortste pad algoritme wordt toegepast. Dijkstra’s algoritme is een soort recept waarmee op systematische wijze de kortste route gevonden kan worden tussen een begin- en eindpunt op een graaf. Hoe dat precies werkt lees je in dit artikel.

Bruggers ontwijken

Met de aanpak die we nu hebben bedacht kunnen we kortste route vinden, uitgaand van ideale omstandigheden. Dat wil zeggen dat er geen rekening gehouden wordt met files. Als je dus van de aula naar de wiskundeles liever niet in een grote meute bruggers belandt, moeten we wat anders bedenken.

Tot nu toe hebben we gewerkt met vaste waarden als gewichten (de looptijden bij een gemiddelde loopsnelheid). Tijdens de masterclass van NETWORKS werd het idee geïntroduceerd om zogeheten vertragingsfuncties te gebruiken. Een vertragingsfunctie is een "dynamisch gewicht": het geeft de looptijd van een zijde als functie van de stroom over deze zijde; veel bruggers betekent een langere looptijd. Doordat de drukte het gewicht aanpast, verandert de snelste route. Het programma houdt dus rekening met drukte!

Een lange zoektocht door de fundamenten van toegepaste verkeerstheorie brengt ons bij de functie van Kladek, die de relatie tussen snelheid en stroomdichtheid beschrijft. Hieruit kunnen we een formule afleiden die direct de looptijd als functie van het aantal voetgangers geeft.

Klik hier om meer te lezen over het model van Kladek en de vertragingsfunctie die we daarmee hebben afgeleid.

Dit is het model dat Kladek (1966) voorstelde om de relatie tussen dichtheid en snelheid van een stroom te beschrijven:
\begin{equation} v = v_f \left(1 - e^{-\gamma\left(\frac{1}{k'} - \frac{1}{k'_\text{jam}} \right)} \right) \end{equation}
De variabele $v$ is de daadwerkelijke loopsnelheid en $v_f$ de vrije loopsnelheid (de loopsnelheid als er niemand anders om je heen is). De variabele $k'$ is de dichtheid van een stroom en $k'_\text{jam}$ de dichtheid waarbij de stroom tot stilstand komt. Dus: de dichtheid waarbij het zo druk is, dat alles stil komt te staan.

We weten dat de dichtheid van een stroom gegeven wordt door
\begin{equation} k' = \frac{n}{x \cdot y}. \end{equation}
$n$ [ $P$ ] is het aantal personen op een zijde
$x$ [ $m$ ] is de breedte van de zijde
$y$ [ $m$ ] is de lengte van de zijde

Het gewicht van een zijde is de tijd die het kost om het segment te bewandelen. Met een constante wandelsnelheid is dat

\begin{equation} w = \frac{y}{v_\mu}. \end{equation}

In het geval van voetgangersstromen is de vrije loopsnelheid gelijk aan de gemiddelde loopsnelheid:
\begin{equation} v_f = v_\mu = 1,34 m/s. \end{equation}

Nu verandert de loopsnelheid. We rekenen de gewichten dus niet uit met $v_f$ , maar met $v$ . We spreken dan niet meer over het gewicht maar over vertraging $L_e(n)$ op zijde $e$ bij $n$ voetgangers op het segment:
\begin{equation}
\begin{split}
L_e(n) = \frac{y}{v} &= \frac{y}{v_f \left(1 - e^{-\gamma\left(\frac{1}{k'} - \frac{1}{k'_\text{jam}} \right)} \right)} \\ &= \frac{w}{\left(1 - e^{-\gamma\left(\frac{x w v_f}{n} - \frac{1}{k'_\text{jam}} \right)} \right)}. \end{split} \end{equation}.
In de laatste stap substitueren we $v_f$ met $v_\mu$ en herkennen we de formule voor het origenele gewicht $w$ van de zijde. Daarnaast substitueren we $k'$ .

Hieronder een grafiek van de bovenstaande functie:

Echter zien we dat, als de dichtheid van een stroom boven de maximale dichtheid uitgaat, de vertraging negatief wordt. Ook is de vertraging ongedefinieerd bij
n=0. We moeten dus een paar uitzonderingen aan de formule toevoegen. De eindformule is:

\begin{equation}
L_e(n) = \begin{cases}w & \text{als $n=0$,} \\
\frac{w}{\left(1 - e^{-\gamma\left(\frac{1}{k'} - \frac{1}{k'_\text{jam}} \right)} \right)} & \text{als $0 < n < xwv_fk'_\text{jam}$,} \\ \infty & \text{als $n \geq xwv_fk'_\text{jam}$.}\end{cases} \end{equation} $n$ [ $P$ ] is het aantal personen op een zijde
$L_e$ [ $s$ ] is de vertraging van een zijde
$x$ [ $m$ ] is de breedte van de zijde
$y$ [ $m$ ] is de lengte van de zijde
$w$ [ $s$ ] is het gewicht van een zijde
$k'$ [ $P/m^2$ ] is de stroomdichtheid, met $k'_\text{jam}=5,4 P/m^2$ als maximale dichtheid is een constante

Naast de vertragingsfuncties moeten we ook kijken naar het Nash-equilibrium, maar wat is dat? Stel dat alle Amsterdammers ineens besluiten om een dagje naar Leeuwarden te gaan. De meest voordehandliggende routes gaan via de A6 (door Flevoland) of via de A7 (over de Afsluitdijk). Natuurlijk gaat niet iedereen via de A6 want dan zou het helemaal vast staan, ook zou niet iedereen over de A7 gaan. In de realiteit vindt de autostroom een evenwicht waarbij beide routes even lang duren en het voor niemand lucratief zou zijn om te wisselen van route. Dit is het Nash-equilibrium, de stroom die daarbij hoort heet de Nash-stroom. In een geval met twee routes en één startpunt en één eindpunt kan dit evenwicht relatief eenvoudig algebraïsch berekend worden.

Wil je eerst de formele definities van stromen en vertragingen lezen, klik dan hier.

Een pad $P$ (of een route) tussen een startpunt $s$ en eindpunt $t$ is een een geordende lijst (of vector) met aaneengesloten vertices, zodanig dat geen enkele vertex twee keer voorkomt in de lijst. Een deelstroom is een waarde tussen (en inclusief) 0 en 1 die wordt toegewezen aan een pad.

Aan elk pad $P_i$ van $s$ naar $t$ wijzen we dus een deelstroom toe die we noteren als $f_{Pi}$ .

Alle deelstromen samen, zeg dat er $k$ zijn, vormen de stroom:
\begin{equation} f := (f_{P1}, f_{P2}, \dots, f_{Pk}). \end{equation}
Een belangrijke voorwaarde is dat al deze deelstromen samen optellen tot één:
\begin{equation} \sum_{f_{Pi} \in f} f_{Pi} = 1. \end{equation}
Een vertragingsfunctie geeft een positief reëel getal (dat is dus de vertraging) aan de deelstroom over. We noteren de vertraging over zijde $e$ wanneer deelstroom $f$ over de zijde loopt als $L_e(f)$ .

De totale vertraging over een pad is de optelsom van de vertragingen van alle zijden over dat pad:
\begin{equation} L_{Pi}(f_{Pi}) = \sum_{e \in P_i} L_e(f_e).\end{equation}
Voor de Nash-stroom geldt dat over elk pad de vertraging gelijk is, dus er geldt:
\begin{equation}L_{P1}(f_{P1}) =L_{P2}(f_{P2}) = \dots = L_{Pk}(f_{Pk}). \end{equation}

Een belangrijke kanttekening in deze definities is dat we ervan uitgaan dat de paden $P_1, P_2, \dots, P_k$ geen overlappende zijden hebben. Hebben ze dat wel, dan worden de wiskundige definities complexer om tot de juiste resultaten te komen. Kun je bedenken waar het fout gaat bij overlappende paden?

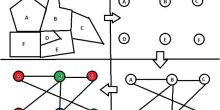
Zie het volgende netwerk en bijbehorende vertragingsfunctie van elke zijde:

Laten we, als oefening, de Nash-stroom tussen s en t uitrekenen. We zien dat er twee paden zijn van $s$ naar $t$ , namelijk $P_1=(s,u,t)$ en $P_2=(s,v,t)$ . De Nash-stroom zal dus uit twee deelstromen bestaan die beide over één pad gaan: $f_\text{nash}=(f_{P1},f_{P2})$ . Binnen een Nash-stroom heeft niemand baat bij het wisselen van pad. De totale vertraging over beide paden moet gelijk zijn: $L_{P1}(f_{P1})=L_{P2}(f_{P2})$ . Om de Nash-stroom te vinden, moeten we dus de stroom vinden die ervoor zorgt dat de vertragingen over beide paden exact gelijk zijn. Omdat er maar twee mogelijke stromen zijn die samen optellen tot $1$ geldt dat, als $f_{P1}=x$ dan $f_{P2}=1-x$ . Door dit in te vullen in de vertragingsfuncties van de graaf kan de volgende vergelijking worden verkregen: \begin{equation*} x+\frac{1}{16}=\frac{3}{4}+(1-x)^2. \end{equation*} Meegenomen dat $0 \leq x \leq 1$ kan de oplossing $x=\tfrac{3}{4}$ gevonden worden. De Nash-stroom is dus $f_\text{nash}=\left(\tfrac{3}{4},\tfrac{1}{4}\right).$

Ook in ons schoolgebouw lopen er stromen, echter is het vinden van een Nash-stroom hier wat ingewikkelder:

Om te beginnen hebben we tientallen begin- en eindpunten met tientallen routes ertussen, wat een algebraïsche berekening veel lastiger maakt. Probeer in het voorbeeld maar eens de Nash-stroom te vinden als je een zijde toevoegt tussen $u$ en $v$ ,
Daarnaast zijn de deelstromen (over de twee mogelijke routes in het voorbeeld) fracties die samen optellen tot één. De reden dat er gekozen wordt voor een representatie van een continue stroom (reële getallen tussen 0 en 1), in tegenstelling tot een discrete benadering (gehele getallen), is dat verkeersstromen meestal gaan over heel veel voertuigen. De impact van een individuele deelnemer is dan verwaarloosbaar, en dus wordt er gesproken over een fractie van het verkeer. Daarentegen heeft het Hyperion Lyceum slechts 859 leerlingen die in beperkte stromen door de school gaan. is Een discrete benadering is daarom gepaster, maar moeilijker te berekenen
Ook willen we een tijdselement verwerken in de leerlingenstroom. De leerlingenstroom moet alleen lopen in bijvoorbeeld de tijdsperiode tussen het eindigen van de ene les en het begin van de ander, maar niet tijdens een les.

Dit leidt ons tot een benadering door middel van een simulatie. We gaan de leerlingenstromen en de files die zij veroorzaken simuleren met een Python-programma.

Het programma dat wij hebben gemaakt stuurt voortdurend leerlingen hun lokaal uit, vervolgens lopen ze door de school naar hun eindpunt. Ondertussen zorgt hun aanwezigheid in gangen en op trappen voor vertraging op dat stuk, waardoor uiteindelijk (als daar nog veel meer leerlingen lopen) file ontstaat. Deze file laat zich dus zien in hogere gewichten omdat de looptijd door bijvoorbeeld een trap simpelweg hoger is door de file. Deze file-grafen worden gebruikt op de juiste tijden, bijvoorbeeld tussen twee lessen in.

Maar hoe zorgt dit ervoor dat we niet in een meute bruggers belanden? De file uit zich dus in een langere looptijd over bepaalde gebieden, het gewicht van de corresponderende zijde is dus hoger. Dit hogere gewicht heeft invloed op Dijkstra’s algoritme waardoor de snelste route anders loopt. De kortste route is niet altijd meer de snelste route, wat in de werkelijkheid ook zo is. Met deze andere route ontlopen we de bruggers.

Onze webapp

Wij hebben ook een website gemaakt zodat leerlingen ons navigatiesysteem zelf kunnen gebruiken. Een soort Google Maps dus, maar alleen voor onze school. Je kunt de website zelf ook bezoeken. We gebruikten gratis hosting dus het laden kan helaas lang duren. Probeer het hier uit.

Het maken van dit navigatiesysteem was een ingewikkeld maar geweldig project. We hebben veel verschillende onderwerpen uit de wiskunde gebruikt om een programma te ontwikkelen dat de snelste routes vindt waarbij we heel veel geleerd hebben. Daarbij willen we graag ons zelfgemaakte stroommodel uitlichten, dat verbazend realistische resultaten laat zien. Dit hadden wij niet kunnen maken zonder de hulp van NETWORKS. Ook was het maken van een gebruikersvriendelijke website niet makkelijk. Of we nu ooit nog een briefje moeten halen? Waarschijnlijk wel, maar aan de route ligt het niet!

Het profielwerkstuk van Dylan en Tobias kun je hier lezen. De foto bovenaan dit artikel, met Tobias links en Dylan rechts, is genomen bij de uitreiking van de Pythagorasprijs.

Would you like to stay up to date when a new post appears on the Network Pages?

Subscribe to our mailing list